You are here
Quantum-assisted and Quantum-based Communications
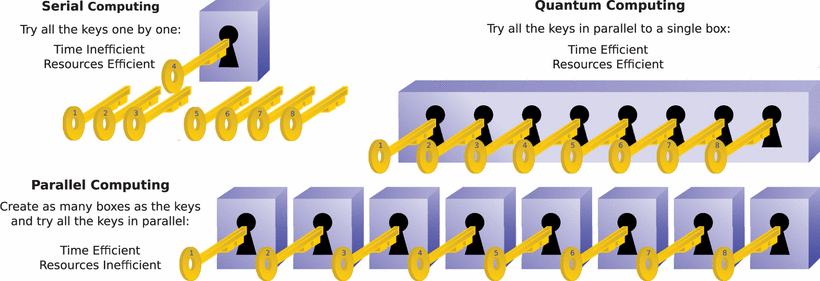
Figure 1. Comparison between classic serial, parallel and quantum computing. Assuming that only one of the eight keys unlocks the box, by employing serial computing we have to try each of the keys sequentially until one succeeds to unlock it. Classic parallel computing creates as many boxes as the available keys and tries all of them at once, requiring a large amount of resources. With quantum computing we are able to try all the keys in parallel on a single box. The box corresponds to a function, while the keys represent the legitimate inputs of the function. The key that unlocks the box is the input of the function which will lead to a desired output. By employing quantum computing, the function may be evaluated for the inputs in parallel, as in parallel computing, with the computational cost of a single evaluation, as in serial computing.
|
Prof Lajos Hanzo, Prof Soon Xin Ng (Michael), Dr Panagiotis Botsinis, Dr Zunaira Babar, Dr Dimitrios Alanis, Dr Hung Nguyen, Dr Daryus Chandra |
|
When quantum computing becomes a wide-spread commercial reality, Quantum Search Algorithms (QSA) and especially Grover’s QSA will inevitably be one of their main applications, constituting their cornerstone. Most of the literature assumes that the quantum circuits are free from decoherence. Practically, decoherence will remain unavoidable as is the Gaussian noise of classic circuits imposed by the Brownian motion of electrons, hence it may have to be mitigated. In this contribution, we investigate the effect of quantum noise on the performance of QSAs, in terms of their success probability as a function of the database size to be searched, when decoherence is modelled by depolarizing channels’ deleterious effects imposed on the quantum gates. Moreover, we employ quantum error correction codes for limiting the effects of quantum noise and for correcting quantum flips. More specifically, we demonstrate that, when we search for a single solution in a database having 4096 entries using Grover’s QSA at an aggressive depolarizing probability of 10?3, the success probability of the search is 0.22 when no quantum coding is used, which is improved to 0.96 when Steane’s quantum error correction code is employed. Finally, apart from Steane’s code, the employment of Quantum Bose-Chaudhuri-Hocquenghem (QBCH) codes is also considered. |
|
Quantum-assisted Multi-User Wireless Systems
Prof Lajos Hanzo, Prof Soon Xin Ng (Michael), Dr Panagiotis Botsinis, Dr Dimitrios Alanis, Dr Zunaira Babar, Dr Hung Nguyen, Dr Daryus Chandra [1] Wireless Myths, Realities, and Futures: From 3G/4G to Optical and Quantum Wireless [2] Quantum Search Algorithms, Quantum Wireless, and a Low-Complexity Maximum Likelihood Iterative Quantum Multi-user Detector Design [3] Low-Complexity Iterative Quantum Multi-User Detection in SDMA Systems [More Publications] |
|
The high complexity of numerous optimal classic communication schemes, such as the maximum likelihood (ML) multiuser detector (MUD), often prevents their practical implementation. In this work, we present an extensive review and tutorial on quantum search algorithms (QSA) and their potential applications, and we employ a QSA that finds the minimum of a function in order to perform optimal hard MUD with a quadratic reduction in the computational complexity when compared to that of the ML MUD. Furthermore, we follow a quantum approach to achieve the same performance as the optimal soft-input soft-output classic detectors by replacing them with a quantum algorithm, which estimates the weighted sum of a function’s evaluations. We propose a soft-input soft-output quantum-assisted MUD (QMUD) scheme, which is the quantum-domain equivalent of the ML MUD. We then demonstrate its application using the design example of a direct-sequence code division multiple access system employing bit-interleaved coded modulation relying on iterative decoding, and compare it with the optimal ML MUD in terms of its performance and complexity. Both our extrinsic information transfer charts and bit error ratio curves show that the performance of the proposed QMUD and that of the optimal classic MUD are equivalent, but the QMUD’s computational complexity is significantly lower. |
|
In a system supporting numerous users the complexity of the optimal Maximum Likelihood Multi-User Detector (ML MUD) becomes excessive. Based on the superimposed constellations of K users, the ML MUD outputs the specific multi-level K-user symbol that minimizes the Euclidean distance with respect to the faded and noise-contaminated received multi-level symbol. Explicitly, the Euclidean distance is considered as the Cost Function (CF). In a system supporting K users employing M-ary modulation, the ML MUD uses M^K CF evaluations (CFE) per time slot. In this contribution we propose an Early Stopping-aided Durr-Hoyer algorithm-based Quantum-assisted MUD (ES-DHA QMUD) based on two techniques for achieving optimal ML detection at a low complexity. Our solution is also capable of flexibly adjusting the QMUD's performance and complexity trade-off, depending on the computing power available at the base station. We conclude by proposing a general design methodology for the ES-DHA QMUD in the context of both CDMA and SDMA systems. |
|
Low-complexity suboptimal multiuser detectors (MUDs) are widely used in multiple access communication systems for separating users, since the computational complexity of the maximum likelihood (ML) detector is potentially excessive for practical implementation. Quantum computing may be invoked in the detection procedure, by exploiting its inherent parallelism for approaching the ML MUDs performance at a substantially reduced number of cost function evaluations. In this contribution, we propose a soft-output (SO) quantum-assisted MUD achieving a near-ML performance and compare it to the corresponding SO ant colony optimization MUD. We investigate rank deficient direct-sequence spreading (DSS) and slow subcarrier-hopping aided (SSCH) spatial division multiple access orthogonal frequency division multiplexing systems, where the number of users to be detected is higher than the number of receive antenna elements used. We show that for a given complexity budget, the proposed SO-Dürr-Høyer algorithm (DHA) QMUD achieves a better performance. We also propose an adaptive hybrid SO-ML/SO-DHA MUD, which adapts itself to the number of users equipped with the same spreading sequence and transmitting on the same subcarrier. Finally, we propose a DSS-based uniform SSCH scheme, which improves the system's performance by 0.5 dB at a BER of 10^(−5), despite reducing the complexity required by the MUDs employed. |
|
In large-dimensional wireless systems, such as Cooperative Multi-cell Processing (CoMP), mm-Wave and massive MIMO systems, or cells having a high user density, such as airports, train stations and metropolitan areas, sufficiently accurate estimation of all the channel gains is required for performing coherent detection. Therefore they may impose an excessive complexity. As an attractive design alternative, differential modulation relying on non-coherent detection may be invoked for eliminating the requirement for channel estimation at the Base Station, although at the cost of some performance degradation. In this treatise we propose low-complexity Hard-Input Hard-Output (HIHO), Hard-Input Soft-Output (HISO), as well as Soft-Input Soft-Output (SISO) Quantum-assisted Multiple Symbol Differential Detectors (QMSDD) which perform equivalently to the optimal, but highly complex Maximum A posteriori Probability (MAP) MSDDs in multi-user systems, where the users are separated both in the frequency domain and in the time domain. When using an MSDD, the detection of a user’s symbols is performed over windows of differentially modulated symbols, hence they exhibit an increased complexity with respect to the Conventional Differential Detector (CDD), while simultaneously improving the performance of the system, especially at high Doppler frequencies. |
|
With the proliferation of smart-phones and tablet PCs, the data rates of wireless communications have been soaring. Hence, the need for power-efficient communications relying on low-complexity multiple-stream detectors has become more pressing than ever. As a remedy, in this paper we design low-complexity soft-input soft-output quantum-assisted multi-user detectors (QMUD), which may be conveniently incorporated into state-of-the-art iterative receivers. Our design relies on extrinsic information transfer charts. Our QMUDs are then employed in multi-carrier interleave-division multiple-access (MC-IDMA) systems, which are investigated in the context of different channel code rate and spreading factor pairs, whilst fixing the total bandwidth requirement. One of our QMUDs is found to operate within 0.5 dB of the classical maximum a posteriori probability MUD after three iterations between the MUD and the decoders, while requiring only half its complexity, at a BER of 10-5 in the uplink of a rank-deficient MC-IDMA system relying on realistic imperfect channel estimation at the receiver, while supporting 14 users transmitting QPSK symbols. |
|
Joint Channel Estimation (CE) and Multi-User Detection (MUD) has become a crucial part of iterative receivers. In this paper we propose a Quantum-assisted Repeated Weighted Boosting Search (QRWBS) algorithm for CE and we employ it in the uplink of MIMO-OFDM systems, in conjunction with the Maximum A posteriori Probability (MAP) MUD and a nearoptimal Quantum-assisted MUD (QMUD). The performance of the QRWBS-aided CE is evaluated in rank-deficient systems, where the number of receive Antenna Elements (AE) at the Base Station (BS) is lower than the number of supported users. The effect of the Channel Impulse Response (CIR) prediction filters, of the Power Delay Profile (PDP) of the channels and of the Doppler frequency have on the attainable system performance is also quantified. The proposed QRWBS-aided CE is shown to outperform the RWBS-aided CE, despite requiring a lower complexity, in systems where iterations are invoked between the MUD, the CE and the channel decoders at the receiver. In a system, where U = 7 users are supported with the aid of P = 4 receive AEs, the joint QRWBS-aided CE and QMUD achieves a 2 dB gain, when compared to the joint RWBS-aided CE and MAP MUD, despite imposing 43% lower complexity. |
|
With the research on implementing a universal quantum computer being under the technological spotlight, new possibilities appear for their employment in wireless communications systems for reducing their complexity and improving their performance. In this treatise, we consider the downlink of a rank-deficient, multi-user system and we propose the discrete-valued and continuous-valued Quantum-assisted Particle Swarm Optimization (QPSO) algorithms for performing Vector Perturbation (VP) precoding, as well as for lowering the required transmission power at the Base Station (BS), while minimizing the expected average Bit Error Ratio (BER) at the mobile terminals. We use the Minimum BER (MBER) criterion. We show that the novel quantum-assisted precoding methodology results in an enhanced BER performance, when compared to that of a classical methodology employing the PSO algorithm, while requiring the same computational complexity in the challenging rank-deficient scenarios, where the number of transmit antenna elements at the BS is lower than the number of users. Moreover, when there is limited Channel State Information (CSI) feedback from the users to the BS, due to the necessary quantization of the channel states, the proposed quantum-assisted precoder outperforms the classical precoder. |
|
Prof Lajos Hanzo, Prof Soon Xin Ng (Michael), Dr Panagiotis Botsinis, Dr Dimitrios Alanis, Dr Simeng Feng, Dr Zunaira Babar, Dr Hung Nguyen, Dr Daryus Chandra
[10] Quantum-Assisted Indoor Localization for Uplink mm-Wave and Downlink Visible Light Communication Systems [More Publications] |
|
With the proliferation of mm-Wave systems and Visible Light Communications (VLC), indoor localization may find multiple applications. When high localization accuracy is required and triangulation is not possible due to the infrastracture and scenario limitations, the computational complexity of searching on a virtual grid may become excessive. In this contribution, we amalgamate uplink mm-Wave-based and downlink VLC-based localization. We employ quantum search algorithms for reducing the computational complexity required for achieving the optimal full-search-based performance. Regarding the uplink mm-Wave-based localization, we employ a single anchor equipped with multiple Antenna Elements (AEs) and we exploit the specular multipath components created by the room’s walls. The proposed solutions outperform the stateof- the-art algorithms. Furthermore, various channel models are considered, based on real indoors mm-Wave measurements. By using VLC-based triangulation for downlink and the proposed mm-Wave-based localization algorithm for uplink, there was an average positioning error of 5.6 cm in the room considered, while requiring 261 database queries on average. |
|
Quantum Error Mitigation
Prof Lajos Hanzo, Prof Soon Xin Ng (Michael), Dr Daryus Chandra, Mr Yifeng Xiong [1] Sampling Overhead Analysis of Quantum Error Mitigation: Uncoded vs. Coded Systems [More Publications] |
|
Quantum error mitigation (QEM) is a promising technique of protecting hybrid quantum-classical computation from decoherence, but it suffers from sampling overhead which erodes the computational speed. In this treatise, we provide a comprehensive analysis of the sampling overhead imposed by QEM. In particular, we show that Pauli errors incur the lowest sampling overhead among a large class of realistic quantum channels having the same average fidelity. Furthermore, we show that depolarizing errors incur the lowest sampling overhead among all kinds of Pauli errors. Additionally, we conceive a scheme amalgamating QEM with quantum channel coding, and analyse its sampling overhead reduction compared to pure QEM. Especially, we observe that there exist a critical number of gates contained in quantum circuits, beyond which their amalgamation is preferable to pure QEM. Figure 2. The workflow of a typical variational algorithm designed for hybrid-quantum classical computation. |
|
QEM is capable of reducing the computational error of variational quantum algorithms tailored for current noisy intermediate-scale quantum computers. The recently proposed permutation-based methods are practically attractive, since they do not rely on any a priori information concerning the quantum channels. In this treatise, we propose a general framework termed as permutation filters, which includes the existing permutation-based methods as special cases. In particular, we show that the proposed filter design algorithm always converges to the global optimum, and that the optimal filters can provide substantial improvements over the existing permutation-based methods in the presence of narrowband quantum noise, corresponding to large-depth, high-error-rate quantum circuits. Figure 3. An n-th order permutation filter proposed in this treatise applied to a variational quantum algorithm. |
|
In general, the computational error reduction capability of QEM comes at the cost of a sampling overhead due to the variance-boosting effect caused by the channel inversion operation, which ultimately limits the applicability of QEM. Existing sampling overhead analysis of QEM typically assumes exact channel inversion, which is unrealistic in practical scenarios. In this treatise, we consider a practical channel inversion strategy based on Monte Carlo sampling, which introduces an additional computational error that in turn may be eliminated at the cost of an extra sampling overhead. In particular, we show that when the computational error is small compared to the dynamic range of the error-free results, it scales with the square root of the number of gates. By contrast, the error exhibits a linear scaling with the number of gates in the absence of QEM under the same assumptions. Hence, the error scaling of QEM remains to be preferable even without the extra sampling overhead. Our analytical results are accompanied by numerical examples. Figure 4. The RMSE of the results computed by quantum circuits carrying out repeated rotations around the X-axis of the Bloch sphere. The RMSE of Monte Carlo-based QEM grows with the square root of the number of gates, while the RMSE of the result without QEM protection increases linearly. |
|
Symmetry verification constitutes a class of QEM techniques, which distinguishes erroneous computational results from the correct ones by exploiting the intrinsic symmetry of the computational tasks themselves. Inspired by the benefits of quantum switch in the quantum communication theory, we propose beneficial techniques for circuit-oriented symmetry verification that are capable of verifying the commutativity of quantum circuits without the knowledge of the quantum state. In particular, we propose the spatio-temporal stabilizer (STS) technique, which generalizes the conventional quantum-domain stabilizer formalism to circuit-oriented stabilizers. The applicability and implementational strategies of the proposed techniques are demonstrated by using practical quantum algorithms, including the quantum Fourier transform (QFT) and the quantum approximate optimization algorithm (QAOA). Figure 5. A Spatio-temporal Stabilizer (STS) which may be used to detect single-qubit Z-errors in the circuit C. |
|
Quantum Error Correction Codes
Prof Lajos Hanzo, Prof Soon Xin Ng (Michael), Dr Zunaira Babar, Dr Hung Nguyen, Dr Daryus Chandra, Dr Panagiotis Botsinis, Dr Dimitrios Alanis [1] Reduced-Complexity Syndrome-Based TTCM Decoding [2] EXIT-chart aided Quantum Turbo Code Design [3] EXIT-Chart Aided Code Design for Symbol-Based Entanglement-Assisted Classical Communication over Quantum Channels [More Publications] |
|
The design of Quantum Turbo Codes (QTCs) typically relies on the analysis of their distance spectra, followed by Monte-Carlo simulations. In this work, we extend the application of EXtrinsic Information Transfer (EXIT) charts to quantum turbo codes, which sets a lower bound on the achievable decoding performance, with the predicted convergence threshold lying only 0.3 dB below the Word Error Rate (WER) simulation results. Furthermore, we have conceived EXIT-chart aided code search algorithms for optimizing QTCs. Using the proposed algorithms, we have designed an optimal entanglement-assisted QTC, whose performance is only 0.4 dB away from the corresponding hashing bound. |
|
We have conceived a near-capacity code design for entanglement-assisted classical communication over the quantum depolarizing channel. The proposed system relies on efficient near-capacity classical code designs for approaching the entanglement-assisted classical capacity of a quantum depolarizing channel. It incorporates an Irregular Convolutional Code (IRCC), a Unity Rate Code (URC) and a soft-decision aided Superdense Code (SD), which is hence referred to as an IRCC-URC-SD arrangement. Furthermore, the entanglement-assisted classical capacity of an N-qubit superdense code transmitted over a depolarizing channel is invoked for benchmarking. It is demonstrated that the proposed system operates within 0.4 dB of the achievable noise limit for both 2-qubit as well as 3-qubit SD schemes. More specifically, our design exhibits a deviation of only 0.062 and 0.031 classical bits per channel use from the corresponding 2-qubit and 3-qubit capacity limits, respectively. The proposed system is also benchmarked against the classical convolutional and turbo codes. |
|
Powerful quantum error correction codes (QECCs) are required for stabilizing and protecting fragile qubits against the undesirable effects of quantum decoherence. Similar to classical codes, hashing bound approaching QECCs may be designed by exploiting a concatenated code structure, which invokes iterative decoding. Therefore, in this paper, we provide an extensive step-by-step tutorial for designing extrinsic information transfer (EXIT) chart-aided concatenated quantum codes based on the underlying quantum-to-classical isomorphism. These design lessons are then exemplified in the context of our proposed quantum irregular convolutional code (QIRCC), which constitutes the outer component of a concatenated quantum code. The proposed QIRCC can be dynamically adapted to match any given inner code using EXIT charts, hence achieving a performance close to the hashing bound. It is demonstrated that our QIRCC-based optimized design is capable of operating within 0.4 dB of the noise limit. |
|
The near-capacity performance of classical low-density parity check (LDPC) codes and their efficient iterative decoding makes quantum LDPC (QLPDC) codes a promising candidate for quantum error correction. In this paper, we present a comprehensive survey of QLDPC codes from the perspective of code design as well as in terms of their decoding algorithms. We also conceive a modified non-binary decoding algorithm for homogeneous Calderbank-Shor-Steane-type QLDPC codes, which is capable of alleviating the problems imposed by the unavoidable length-four cycles. Our modified decoder outperforms the state-of-the-art decoders in terms of their word error rate performance, despite imposing a reduced decoding complexity. Finally, we intricately amalgamate our modified decoder with the classic uniformly reweighted belief propagation for the sake of achieving an improved performance. |
|
Quantum Turbo Codes (QTCs) are known to operate close to the achievable Hashing bound. However, the sequential nature of the conventional quantum turbo decoding algorithm imposes a high decoding latency, which increases linearly with the frame length. This posses a potential threat to quantum systems having short coherence times. In this context, we conceive a Fully- Parallel Quantum Turbo Decoder (FPQTD), which eliminates the inherent time dependencies of the conventional decoder by executing all the associated processes concurrently. Due to its parallel nature, the proposed FPQTD reduces the decoding times by several orders of magnitude, while maintaining the same performance. We have also demonstrated the significance of employing an odd-even interleaver design in conjunction with the proposed FPQTD. More specifically, it is shown that an oddeven interleaver reduces the computational complexity by 50%, without compromising the achievable performance. |
|
Classical row-circulant quasi-cyclic (QC) low-density parity check (LDPC) matrices are known to generate efficient high-rate short and moderate-length QC-LDPC codes, while the comparable random structures exhibit numerous short cycles of length-4. Therefore, we conceive a general formalism for constructing nondual-containing Calderbank-Shor-Steane (CSS)-type quantum low-density parity check (QLDPC) codes from arbitrary classical row-circulant QC-LDPC matrices. We apply our proposed formalism to the classical balanced incomplete block design (BIBD)-based row-circulant QC-LDPC codes for demonstrating that our designed codes outperform their dual-containing CSS-type counterparts as well as the entanglement-assisted (EA)-QLDPC codes. |
|
In this contribution, the Hashing bound of Entanglement Assisted Quantum Channels (EAQC) is investigated in the context of quantum devices built from a range of popular materials, such as trapped ion and relying on solid state Nuclear Magnetic Resonance (NMR), which can be modelled as a so-called asymmetric channel. Then, Quantum Error Correction Codes (QECC) are designed based on Extrinsic Information Transfer (EXIT) charts for improving performance when employing these quantum devices. The results are also verified by simulations. Our QECC schemes are capable of operating close to the corresponding Hashing bound. |
|
Quantum-assisted Routing
Prof Lajos Hanzo, Prof Soon Xin Ng (Michael) , Dr Dimitrios Alanis , Dr Panagiotis Botsinis , Dr Zunaira Babar , Dr Hung Nguyen , Dr Daryus Chandra [1] Quantum-Assisted Routing Optimization for Self-Organizing Networks [2] Non-Dominated Quantum Iterative Routing Optimization for Wireless Multihop Networks [3] Quantum-Assisted Joint Multi-Objective Routing and Load Balancing for Socially-Aware Networks [More Publications] |
|
[1] Quantum-Assisted Routing Optimization for Self-Organizing Networks Video 1. NDQO simulation for a 6-node SON for 300 frames: The SON is assumed to be covering a (100x100) m square block area, where the Source Node (SN) and the Destination Node (DN) are located at the opposite corners of this square block and they are stationary. The Mobile Relay Nodes are denoted in the video by the red triangle marker and are referred to as RI, where we have that I belongs in the set {1,2,3,4. Their initial locations are random, obeying a uniform distribution within the square block area. A new random destination is reached after 100 frames. Each of the RIs and the DN experience Gaussian interference at each random location and the interference power is produced by the complex Gaussian process CN(-90,10) in dBm. Their levels are noted above the marker of each RI and at the bottom legend located at the right hand side of the video. A linear interpolation process is used for simulating the evolution of the levels of interference between the random locations for each RI and the DN. The NDQO algorithm is employed for each frame for the sake of identifying the Pareto Optimal routes in terms of the Bit Error Ratio (BER) and the total power dissipation of each route. The routes are marked in the respective graph with arrows of distinct colors per route. Moreover, QPSK transmissions over uncorrelated Rayleigh channel are assumed and the loss model has a path loss exponent of a=3. A list of the optimal routes is shown in the top legend located at the right hand side of the video clip. [top] Routing in Wireless Multihop Networks (WMHNs) relies on a delicate balance of diverse and often conflicting parameters, when aiming for maximizing the WMHN performance. Classified as a Non-deterministic Polynomial-time hard problem (NP-hard), routing in WMHNs requires sophisticated methods. As a benefit of observing numerous variables in parallel, quantum computing offers a promising range of algorithms for complexity reduction by exploiting the principle of Quantum Parallelism (QP), while achieving the optimum full-search-based performance. In fact, the so-called Non-Dominated Quantum Optimization (NDQO) algorithm has been proposed for addressing the multi-objective routing problem with the goal of achieving a near-optimal performance, while imposing a complexity of the order of O(N) and O(N3/2) in the best- and worst-case scenarios, respectively. However, as the number of nodes in the WMHN increases, the total number of routes increases exponentially, making its employment infeasible despite the complexity reduction offered. Therefore, we propose a novel optimal quantum-assisted algorithm, namely the Non-Dominated Quantum Iterative Optimization (NDQIO) algorithm, which exploits the synergy between the hardware and the quantum parallelism for the sake of achieving a further complexity reduction, which is on the order of O(N1/2) and O(N3/2) in the best- and worst-case scenarios, respectively. Additionally, we provide simulation results for demonstrating that our NDQIO algorithm achieves an average complexity reduction of almost an order of magnitude compared to the near-optimal NDQO algorithm, while having the same order of power consumption. Video 2. A brief introduction into quantum-assisted multi-objective routing. Prof Lajos Hanzo, Prof Soon Xin Ng (Michael), Dr Dimitrios Alanis, Dr Jie Hu, Dr Panagiotis Botsinis, Dr Zunaira Babar
[3] Quantum-Assisted Joint Multi-Objective Routing and Load Balancing for Socially-Aware Networks The widespread use of mobile networking devices, such as smart phones and tablets, has substantially increased the number of nodes in the operational networks. These devices often suffer from the lack of power and bandwidth. Hence, we have to optimize their message routing for the sake of maximizing their capabilities. However, the optimal routing typically relies on a delicate balance of diverse and often conflicting objectives, such as the route's delay and power consumption. The network design also has to consider the nodes' user-centric social behavior. Hence, the employment of socially aware load balancing becomes imperative for avoiding the potential formation of bottlenecks in the network's packet-flow. In this paper, we propose a novel algorithm, referred to as the multi-objective decomposition quantum optimization (MODQO) algorithm, which exploits the quantum parallelism to its full potential by reducing the database correlations for performing multi-objective routing optimization, while at the same time balancing the teletraffic load among the nodes without imposing a substantial degradation on the network's delay and power consumption. Furthermore, we introduce a novel socially aware load balancing metric, namely, the normalized entropy of the normalized composite betweenness of the associated socially aware network, for striking a better tradeoff between the network's delay and power consumption. We analytically prove that the MODQO algorithm achieves the full-search based accuracy at a significantly reduced complexity, which is several orders of magnitude lower than that of the full search. Finally, we compare the MODQO algorithm to the classic non-dominated sort genetic algorithm II evolutionary algorithm and demonstrate that the MODQO succeeds in halving the network's average delay, while simultaneously reducing the network's average power consumption by 6 dB without increasing the computational complexity. |
|
[1] Quantum Approximate Optimization Algorithm Based Maximum Likelihood Detection Recent advances in quantum technologies pave the way for noisy intermediate-scale quantum (NISQ) devices, where the quantum approximation optimization algorithm (QAOA) constitutes a promising candidate for demonstrating tangible quantum advantages based on NISQ devices. In this paper, we consider the maximum likelihood (ML) detection problem of binary symbols transmitted over a multiple-input and multiple-output (MIMO) channel, where finding the optimal solution is exponentially hard using classical computers. Here, we apply the QAOA for the ML detection by encoding the problem of interest into a level-$p$ QAOA circuit having $2p$ variational parameters, which can be optimized by classical optimizers. This level-$p$ QAOA circuit is constructed by applying the prepared Hamiltonian to our problem and the initial Hamiltonian alternately in $p$ consecutive rounds. More explicitly, we first encode the optimal solution of the ML detection problem into the ground state of a problem Hamiltonian. Using the quantum adiabatic evolution technique, we provide both analytical and numerical results for characterizing the evolution of the eigenvalues of the quantum system used for ML detection. Then, for level-1 QAOA circuits, we derive the analytical expressions of the expectation values of the QAOA and discuss the complexity of the QAOA based ML detector. Explicitly, we evaluate the computational complexity of the classical optimizer used and the storage requirement of simulating the QAOA. Finally, we evaluate the bit error rate (BER) of the QAOA based ML detector and compare it both to the classical ML detector and to the classical minimum mean squared error (MMSE) detector, demonstrating that the QAOA based ML detector is capable of approaching the performance of the classical ML detector.
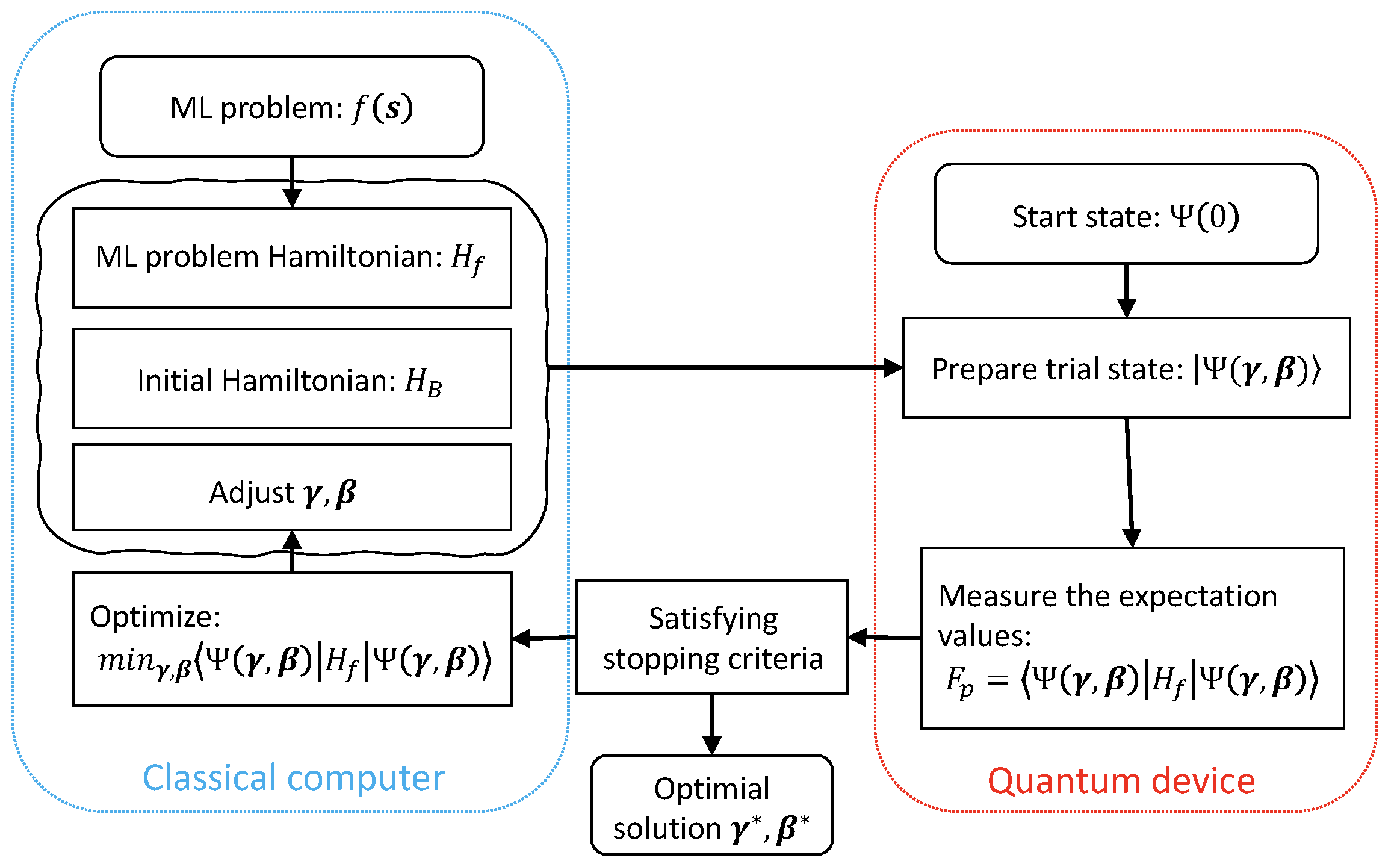
Fig.1 The QAOA diagram for optimizing $F_p$
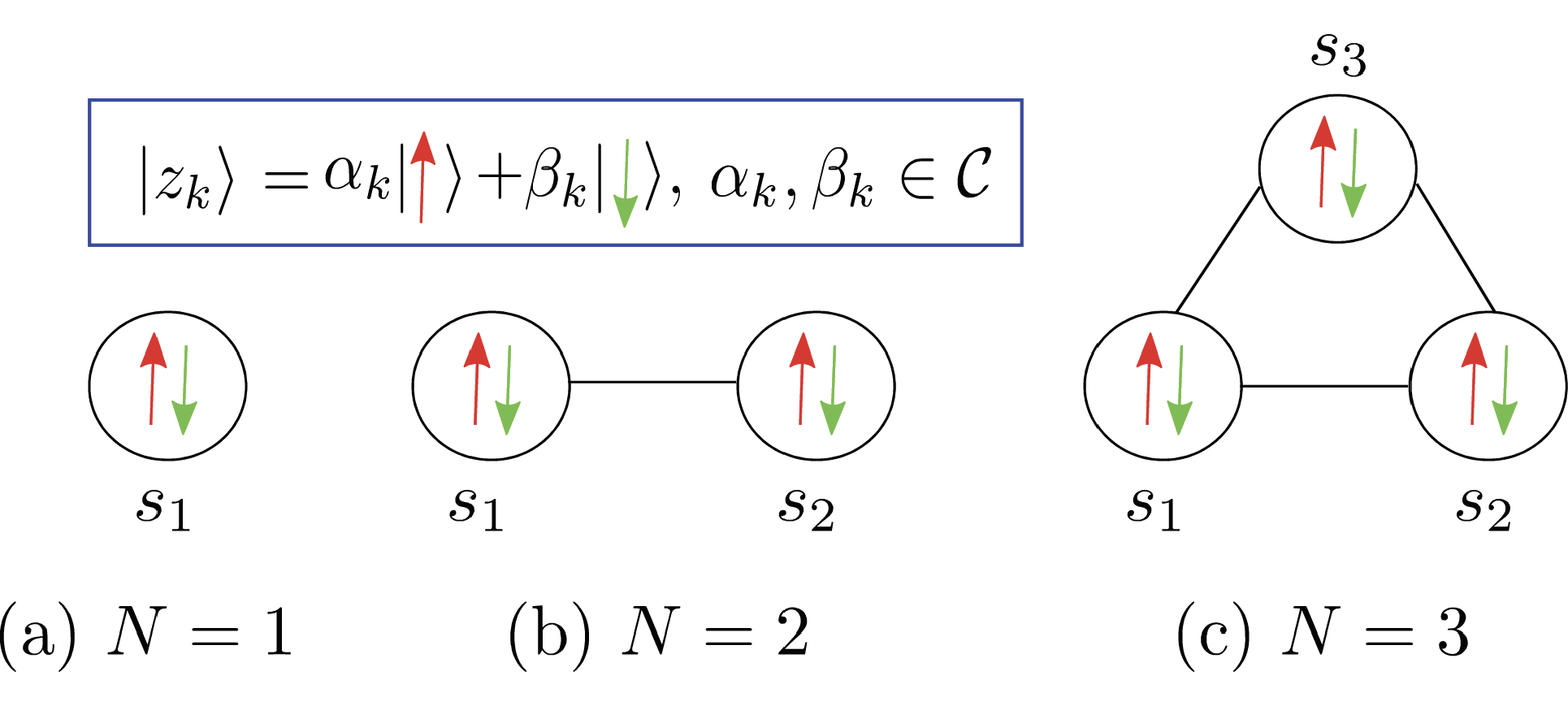
Fig.2 An example of the connections between different symbols received in a MIMO system with BPSK [2] General Hamiltonian Representation of ML Detection Relying on the Quantum Approximate Optimization Algorithm As an extension of the research on binary symbols, a general quantum detection framework is developed for obtaining the ML solution by quantum algorithms. we solve the maximum likelihood (ML) detection problem for general constellations by appropriately adapting the QAOA, which gives rise to a new paradigm in communication systems. We first transform the ML detection problem into a weighted minimum $N$-satisfiability (WMIN-$N$-SAT) problem, where we formulate the objective function of the WMIN-$N$-SAT as a pseudo Boolean function. Furthermore, we formalize the connection between the degree of the objective function and the Gray-labelled modulation constellations. Explicitly, we show a series of results exploring the connection between the coefficients of the monomials and the patterns of the associated constellation points, which substantially simplifies the objective function with respect to the problem Hamiltonian of the QAOA. In particular, for an M-ary Gray-mapped quadrature amplitude modulation (MQAM) constellation, we show that the specific qubits encoding the in-phase components and those encoding the quadrature components are independent in the quantum system of interest, which allows the in-phase and quadrature components to be detected separately using the QAOA. Furthermore, we characterize the degree of the objective function in the WMIN-$N$-SAT problem corresponding to the ML detection of multiple-input and multiple-output (MIMO) channels. Finally, we evaluate the approximation ratio of the QAOA for the ML detection problem of quadrature phase shift keying (QPSK) relying on QAOA circuits of different depths.
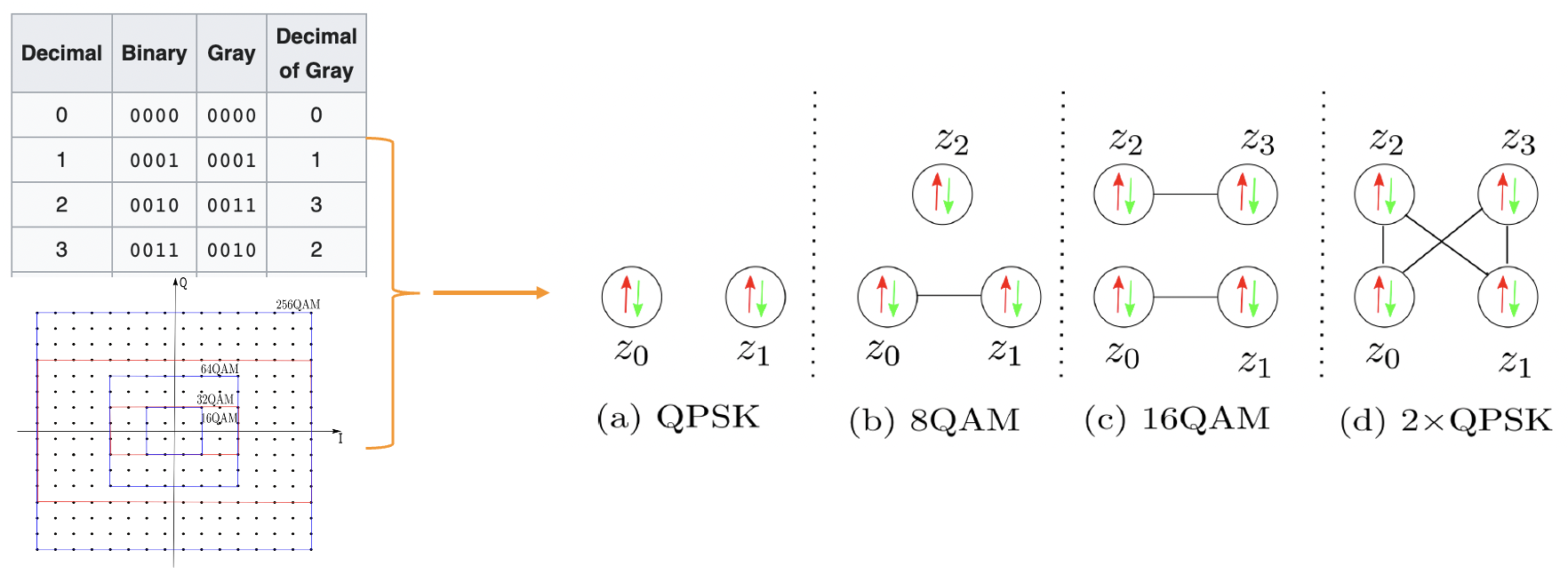
Fig. 3 Gray Mapping Simplifies Problem Hamiltonian
|